Next: Series Up: Sequences and Series Previous: Sequences and Series Contents Index
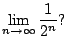
You may have encountered sequences long ago in earlier courses and they seemed very difficult. You know much more mathematics now, so they will probably seem easier. On the other hand, we're going to go very quickly.
| We will completely skip several topics from Chapter 11. I will try to make what we skip clear. Note that the homework has been modified to reflect the omitted topics. |
A sequence is an ordered list of numbers. These numbers may be real, complex, etc., etc., but in this book we will focus entirely on sequences of real numbers. For example,
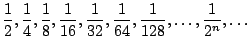
Since the sequence is ordered, we can view it as a function
with domain the natural numbers
![]() .
.
For example,
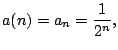
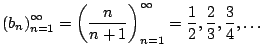
Let's return to the sequence
![]() .
We write
.
We write
![]() , since the terms get arbitrarily
small.
, since the terms get arbitrarily
small.
As a corollary, note that this implies that all the facts about limits that you know from functions also apply to sequences!
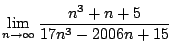 .
Answer:
.
Answer:
William Stein 2006-03-15