Next: Average Values Up: Applications to Areas, Volume, Previous: Examples Contents Index
But what if our solid object looks like a complicated blob? How would we compute the volume? We'll do something that by now should seem familiar, which is to chop the object into small pieces and take the limit of approximations.
[[Picture of solid sliced vertically into a bunch of vertical thin solid discs.]]
Assume that we have a function
| volume of blob | 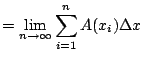 |
|
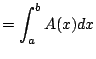 |
For convenience look at pyramid on its side, with the tip of the
pyramid at the origin. We need to figure out the cross sectional area
as a function of ![]() , for
, for
![]() . The function that gives
the distance
. The function that gives
the distance ![]() from the
from the ![]() axis to the edge is a line, with
axis to the edge is a line, with
![]() and
and
![]() . The equation of this line is thus
. The equation of this line is thus
![]() . Thus the cross sectional area is
. Thus the cross sectional area is
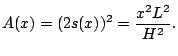
![$\displaystyle \int_{0}^{H} A(x)dx =
\int_{0}^{H} \frac{x^2L^2}{H^2} dx
= \left[ \frac{x^3L^2}{3H^2}\right]_{0}^H
= \frac{H^3L^2}{3H^2} = \frac{1}{3} HL^2.
$](img221.png)
| Today: Quiz!
Next: Polar coordinates, etc. Questions:? Recall: Find volume by integrating cross section of area. (draw picture) |
The cross section is a ``washer'', and the area as a function
of ![]() is
is
![$\displaystyle \int_{0}^1 A(x) dx = \int_{0}^1 \left(\frac{1}{5}x^5 - \frac{1}{7...
...= \pi \left[\frac{1}{5}x^5 - \frac{1}{7}x^7\right]_{0}^{1}
= \frac{2}{35}\pi.
$](img228.png)
![$\displaystyle \frac{1}{2} V = \int_{0}^r \pi (r^2-x^2) dx
= \pi \left[ r^2 x - \frac{1}{3}x^3\right]_0^r
= \pi r^3 - \frac{1}{3} \pi r^3 = \frac{2}{3}\pi r^3.
$](img233.png)
From the picture we see that the answer is
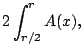
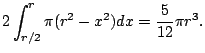
William Stein 2006-03-15