Smith Normal Form

On the first day of class we learned about Smith normal forms of matrices.

> A := Matrix(2,2,[1,2,3,4]);
> A;
[1 2]
[3 4]
> SmithForm(A);
[1 0]
[0 2]

[ 1  0]
[-1  1]

[-1  2]
[ 1 -1]

As you can see, computed the Smith form, which is 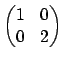$\left( \begin{matrix}1&0\ 0&2 \end{matrix}\right)$. What are the other two matrices it output? To see what any command does, type the command by itself with no arguments followed by a semicolon.

> SmithForm;
Intrinsic 'SmithForm'

Signatures:

    (<Mtrx> X) -> Mtrx, AlgMatElt, AlgMatElt
    [
        k: RngIntElt, 
        NormType: MonStgElt, 
        Partial: BoolElt, 
        RightInverse: BoolElt
    ]

        The smith form S of X, together with unimodular matrices 
        P and Q such that P * X * Q = S.

As you can see, SmithForm returns three arguments, a matrix and matrices $P$ and $Q$ that transform the input matrix to Smith normal form. The syntax to ``receive'' three return arguments is natural, but uncommon in other programming languages:

> S, P, Q := SmithForm(A);
> S;
[1 0]
[0 2]
> P;
[ 1  0]
[-1  1]
> Q;
[-1  2]
[ 1 -1]
> P*A*Q;
[1 0]
[0 2]

Next, let's test the limits. We make a $10\times 10$ integer matrix with entries between 0 and $99$, and compute its Smith normal form.

> A := Matrix(10,10,[Random(100) : i in [1..100]]);
> time B := SmithForm(A);  
Time: 0.000

Let's print the first row of $A$, the first and last row of $B$, and the diagonal of $B$:

> A[1];
( 4 48 84  3 58 61 53 26  9  5)
> B[1];
(1 0 0 0 0 0 0 0 0 0)
> B[10];
(0 0 0 0 0 0 0 0 0 51805501538039733)
> [B[i,i] : i in [1..10]];
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 51805501538039733 ]

Let's see how big we have to make $A$ in order to slow down . These timings below are on a 1.6Ghz Pentium 4-M laptop running Magma V2.11 under VMware Linux. I tried exactly the same computation running Magma V2.17 natively under Windows XP on the same machine, and it takes twice as long to do each computation, which is strange.

> n := 50; A := Matrix(n,n,[Random(100) : i in [1..n^2]]);
> time B := SmithForm(A);  
Time: 0.050
> n := 100; A := Matrix(n,n,[Random(100) : i in [1..n^2]]);
> time B := SmithForm(A);  
Time: 0.800
> n := 150; A := Matrix(n,n,[Random(100) : i in [1..n^2]]);
> time B := SmithForm(A);  
Time: 4.900
> n := 200; A := Matrix(n,n,[Random(100) : i in [1..n^2]]);
> time B := SmithForm(A);  
Time: 19.160

can also work with finitely generated abelian groups.

> G := AbelianGroup([3,5,18]);
> G;
Abelian Group isomorphic to Z/3 + Z/90
Defined on 3 generators
Relations:
    3*G.1 = 0
    5*G.2 = 0
    18*G.3 = 0
> #G;
270
> H := sub<G | [G.1+G.2]>;
> #H;
15
> G/H;
Abelian Group isomorphic to Z/18