


Next: New reading and problems
Up: Freshman Seminar 21n: Elliptic
Previous: Freshman Seminar 21n: Elliptic
Your reading for this coming week is about points of finite order and
how to
work modulo 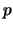 . The first section of chapter 2 characterizes the
points of order
. The first section of chapter 2 characterizes the
points of order 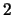 or
or 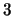 on an elliptic curve, and the second
sectoin discusses the analytic way of viewing an elliptic curve as a
complex torus. This analytic point of view makes it easy to see that
the group of points of order dividing
on an elliptic curve, and the second
sectoin discusses the analytic way of viewing an elliptic curve as a
complex torus. This analytic point of view makes it easy to see that
the group of points of order dividing 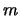 on an elliptic curve is
isomorphic to
on an elliptic curve is
isomorphic to
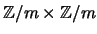 . Section 3 contains some remarks
about discriminants of cubics that are useful in the theorem that
bounds torsion points, which you will read about next week. The
reading from the appendix is concerned with how to define a reduction
map from
. Section 3 contains some remarks
about discriminants of cubics that are useful in the theorem that
bounds torsion points, which you will read about next week. The
reading from the appendix is concerned with how to define a reduction
map from
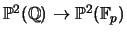 . If
. If 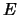 is an elliptic
curve with discriminant not divisible by
is an elliptic
curve with discriminant not divisible by 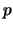 , this map induces a group
homomorphism
, this map induces a group
homomorphism
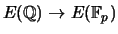 .
.
You should also read a proof that every finitely generated abelian
group can be written as a product of cyclic groups.
William A Stein
2003-02-18