Projective Space

The following is a completely general definition of projective space.

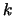
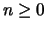
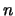
Definition 1.1 (Projective Space)   Let $k$ be a field and $n\geq 0$ an integer. Then $n$ dimensional projective space is, as a set,

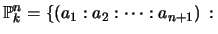
$$\P ^n_k = \{(a_1 : a_2 : \cdots : a_{n+1}) \, : \,$$    not all $a_i=0$ $$\}/\sim,$$

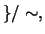
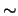
where $\sim$ is the equivalence relation in which

$$(a_1 : a_2 : \cdots : a_{n+1}) \sim (c a_1 : c a_2 : \cdots : c a_{n+1})$$

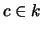
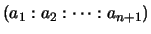
for all nonzero $c\in k$. (Think of $(a_1 : a_2 : \cdots : a_{n+1})$ as a ratio.)

When $k$ has a topology, $\P ^n_k$ inherits a topology (as a quotient of $k^{n-1}-0$) which we probably won't worry about much in this course.

1. The projective space of dimension 0 is a single point.
2. The projective line $\P ^1_k$ is, as a set,
   $$\{ (a_1:a_2) \, : \, a_1, a_2 \in k \} / \!\sim\,\,\, =\, \{ (1 : a) \, : \, a \in k \} \cup \{ (0:1)\}.$$
   Thus the projective line is the usual line union one extra point $(0,1)$, which we often think of as being ``at infinity''.
   1. The set $\P ^1_{\mathbb{R}}$ is the real line along with one extra point at infinity; thus $\P ^1_{\mathbb{R}}$ is in bijection with a circle.
   2. The set $\P ^1_{\mathbb{C}}$ is equal to the complex plane  ${\mathbb{C}}$ along with one extra point at infinity. Alternatively, $\P ^1_{\mathbb{C}}$ can be thought of as the points on the sphere with the north pole corresponding to the point at infinity.
3. When $n=2$ we obtain the projective plane:
   $$\{ (a_1 : a_2 : 1) \, : \, a_1, a_2 \in k \} \cup \{ (1 : a : 0) \, : \, a \in k \} \cup \{ (0 : 1 : 0) \}.$$
   We can think of $\P ^2_k$ as the usual plane along with a copy of $\P ^1_k$ ``at infinity''. The real projective plane $\P ^2_{\mathbb{R}}$ looks like a plane union a circle at infinity. The complex projective plane $\P ^2_{\mathbb{C}}$ has real dimension $4$ so it is harder to describe, but it is where we will primarily work.
4. In general, $\P ^n_k$ is usual $n$-dimension space along with a $\P ^{n-1}_k$ ``at infinity''.

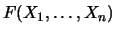
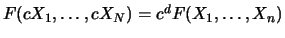
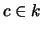
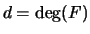
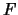
Definition 1.2 (Homogeneous Polynomial)   A homogeneous polynomial is a polynomial $F(X_1,\ldots,X_n)$ such that $F(c X_1,\ldots, c X_N) = c^d F(X_1,\ldots, X_n)$ for all $c\in k$, where $d = \deg(F)$. Equivalently, each of the monomials in $F$ have the same degree.

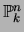
Definition 1.3 (Algebraic Variety)   An algebraic variety in $\P ^n_k$ is the set of solutions to a system

$$F_1(X_1,\ldots,X_{n+1}) = \cdots = F_r(X_1,\ldots,X_{n+1}) = 0$$

of homogeneous polynomial equations. The homogeneity condition ensures that this set is well defined.

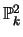
Definition 1.4 (Algebraic Plane Curve)   An algebraic curve in $\P ^2_k$ is the set of solutions to a single nonconstant homogenous polynomial equation

$$\{(a:b:c) : F_1(a,b,c) = 0\}.$$