Let ![]() be the largest degree of any monomial that occurs
in
be the largest degree of any monomial that occurs
in ![]() . E.g.,
. E.g.,
![]() .
.
Simplest case: degree ![]()
Since ![]() , at least one of
, at least one of ![]() . Without loss,
suppose that
. Without loss,
suppose that ![]() . Then
. Then
Next case: degree 2
The graph of ![]() is a conic. (Ellipse, hyperbola, ...)
(A line usually meets the graph in
is a conic. (Ellipse, hyperbola, ...)
(A line usually meets the graph in ![]() points.)
points.)
Such an equation may or may not have solutions unlike
the linear case (when ![]() always has a solution).
always has a solution).
Fact: ![]() has either no solutions or infinitely many.
has either no solutions or infinitely many.
Examples
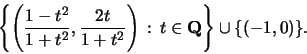
Fact: (mostly explained in Silverman-Tate):
When ![]() has degree
has degree ![]() , the equation
, the equation ![]() has infinitely many solutions (which we can easily parameterize)
if and only if it has at least one solution.
has infinitely many solutions (which we can easily parameterize)
if and only if it has at least one solution.
Example:
Proof:
![]() has a rational solution if and only
if
has a rational solution if and only
if ![]() has a solution with
has a solution with
![]() and
and ![]() (i.e., there is no prime that
simultaneously divides all three of
(i.e., there is no prime that
simultaneously divides all three of ![]() ,
, ![]() ,
, ![]() ).
Suppose that
).
Suppose that ![]() is such a solution. Then
is such a solution. Then
There is a theory that allows one to decide quickly
whether or not a quadratic equation ![]() has
a solution. I will not discuss it further here, but
we can learn more about it in this seminar, if you want.
has
a solution. I will not discuss it further here, but
we can learn more about it in this seminar, if you want.