Proof.
For any
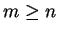
, the number
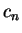
is a partial convergent of
![$ [a_0, \ldots, a_m]$](img57.png)
.
Recall from the previous lecture that the even convergents
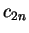
form a strictly
increasing sequence and the odd convergents
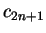
form a strictly
decreasing sequence. Moreover, the even convergents are all
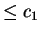
and the odd convergents are all
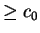
.
Hence
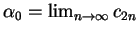
and
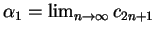
both exist and
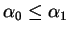
.
Finally, by a proposition from last time
so
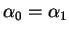
.

Example 2.2
We use PARI to illustrate the convergence of the theorem for
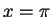
.
? a = contfrac(Pi)
%38 = [3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, ...]
? c = convergents(a)
%39 = [3, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, ...]
? \p9 \\ so we can see.
realprecision = 9 significant digits
? [c[1]*1.0, c[3]*1.0, c[5]*1.0, c[7]*1.0] \\ odd ones converge up to pi
%43 = [3.00000000, 3.14150943, 3.14159265, 3.14159265]
? [c[2]*1.0,c[4]*1.0,c[6]*1.0,c[8]*1.0] \\ even ones swoop down on pi.
%44 = [3.14285714, 3.14159291, 3.14159265, 3.14159265]
Proof.
If the sequence is finite then some
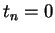
and the
result follows by Proposition
1.2.
Suppose the sequence is infinite.
By Proposition
1.2,
By a proposition from the last lecture
1,
Thus if
![$ c_n = [a_0, a_1, \ldots, a_n]$](img73.png)
, then
Thus
(In the inequality we use that
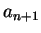
is the integer part of
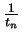
, and
is hence
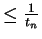
.)

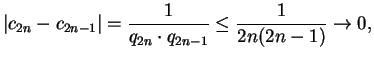
![$\displaystyle x = [a_0, a_1, \ldots, a_n, \frac{1}{t_n}].
$](img71.png)
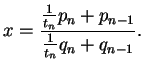
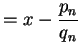
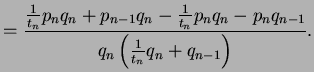
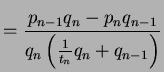
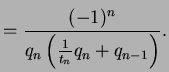
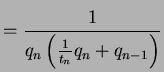
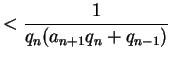
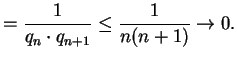
![]()