Next: About this document ...
Math 124 Problem Set 1
1. First, we show that the binomial coefficient is an
integer.
Claim: For fixed 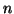 and
and
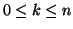 ,
,
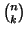 is an integer.
is an integer.
Proof. By
induction. Clearly
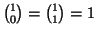 . Suppose
that
. Suppose
that
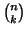 is an integer for
is an integer for
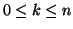 . Now
. Now
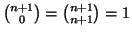 and for
and for
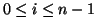
which by the inductive hypothesis is the sum of two integers.
This proves the claim.
Since 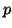 is prime, it is
sufficient to show that there is no factor of
is prime, it is
sufficient to show that there is no factor of 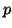 in the
denominator. By assumption,
in the
denominator. By assumption, 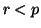 so
so 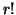 does not contain a
factor of
does not contain a
factor of 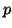 . Similarly,
. Similarly, 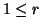 implies that
implies that
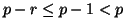 , so
, so 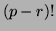 also contains no factor of
also contains no factor of 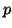 .
.
2.
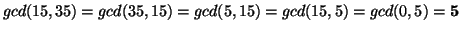 ;
;
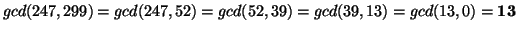 ;
;
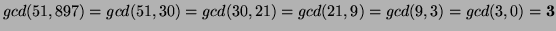 ;
;
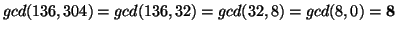 ;
;
3a. The base case is trivial. Suppose that
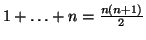 for some
for some 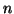 . Then
as
desired.
. Then
as
desired.
3b.If 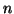 is even we may the group the
terms as
is even we may the group the
terms as
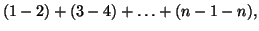 yielding the formula
yielding the formula
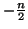 . Similarly, if
. Similarly, if 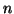 is odd we have
is odd we have
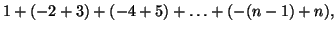 which gives the formula
which gives the formula
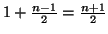 .
.
Therefore the general
formula is
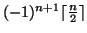 .
.
4. We can run
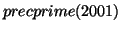 in PARI, which gives
in PARI, which gives
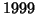 .
.
5. The Euclidean Algorithm gives us:
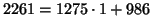 ;
;
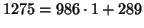 ;
;
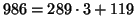 ;
;
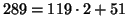 ;
;
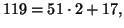 so
so
6.
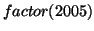 yields
yields 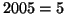 x
x  .
.
7.
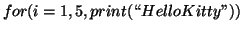
8. A necessary condition is that the polynomial 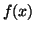 is irreducible over Z; this would include the condition
that the gcd of the coefficients is 1. Certainly if
is irreducible over Z; this would include the condition
that the gcd of the coefficients is 1. Certainly if 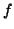 is
reducible then each factor could take the value 1 only a finite
number of times (hence
is
reducible then each factor could take the value 1 only a finite
number of times (hence 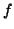 can be prime only at a finite number
of integers). In the case where
can be prime only at a finite number
of integers). In the case where 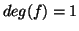 Dirichlet's theorem
confirms that
Dirichlet's theorem
confirms that 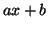 will take infinitely many prime values if
will take infinitely many prime values if
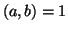 , and in class the conjecture for
, and in class the conjecture for
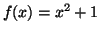 was
presented.
was
presented.
To test a given 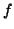 , we could use the
following PARI code:
and then try
, we could use the
following PARI code:
and then try 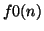 for large values of
for large values of 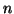 . I tried this for
some cyclotomic polynomials:
. I tried this for
some cyclotomic polynomials: 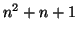 ,
, 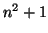 ,
,
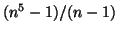 and also for
and also for 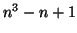 for
for 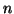 up to 10 billion. All returned
values close to the input. For example, for
up to 10 billion. All returned
values close to the input. For example, for 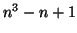 the call
to
the call
to
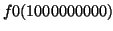 gave 999999986. This suggests that for these
polynomials the conjecture may be true, although it sheds little
light on the general case of irreducible polynomials.
gave 999999986. This suggests that for these
polynomials the conjecture may be true, although it sheds little
light on the general case of irreducible polynomials.
9. We can show that the Euclidean Algorithm on 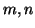 takes
takes
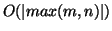 modular operations, where
modular operations, where
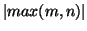 is
the number of binary digits of
is
the number of binary digits of 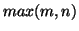 . This is done by noting
that if we proceed from
. This is done by noting
that if we proceed from 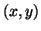 to
to
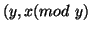 (where
(where 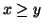 ) then
) then
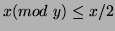 . For if
. For if
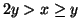 then
then
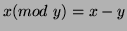 . Combining this with
. Combining this with 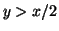 yields
yields
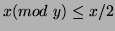 .
Similarly, if
.
Similarly, if 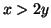 then
then
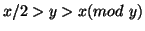 . Therefore every two
steps the original binary representation of
. Therefore every two
steps the original binary representation of 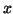 is reduced by one
digit.
is reduced by one
digit.
Now since 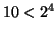 , a
, a 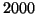 digit number has
fewer than
digit number has
fewer than 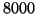 bits, so PARI can easily compute the gcd of two
such numbers.
bits, so PARI can easily compute the gcd of two
such numbers.
10. First we note that all odd integers must be
congruent to 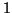 ,
, 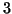 or
or 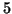 modulo
modulo 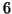 , and if
, and if
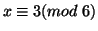 then
then 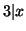 . Therefore all odd primes (except 3) must be
congruent to
. Therefore all odd primes (except 3) must be
congruent to 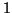 or
or 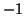 modulo
modulo 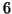 . Next we note that if
. Next we note that if
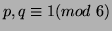 then
then
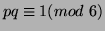 . Therefore if
. Therefore if
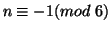 then
then 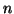 must have a prime factor
must have a prime factor
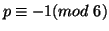 (3 has no inverse).
(3 has no inverse).
Let
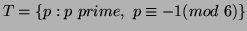 . Suppose
. Suppose 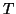 is finite. Since
is finite. Since 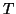 is nonempty (
is nonempty (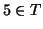 ), we can define
), we can define 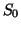 ,
the product of elements in
,
the product of elements in 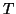 . Now consider
. Now consider 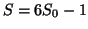 . Since
. Since
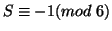 ,
, 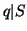 for some
for some 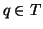 . But for all
. But for all 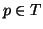 ,
,
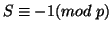 , a contradiction. Therefore
, a contradiction. Therefore 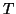 is
infinite.
is
infinite.
11a. We can define a function which computes 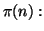 which gives
which gives
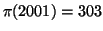 .
.
11b. For 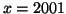 ,
,
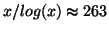 , so the
values differ by about
, so the
values differ by about 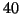 .
.



Next: About this document ...
William A Stein
2001-10-11
![]() and
and
![]() ,
,
![]() is an integer.
is an integer. ![]() . Suppose
that
. Suppose
that
![]() is an integer for
is an integer for
![]() . Now
. Now
![]() and for
and for
![]()