


Next: About this document ...
Homework Assignment 1
Due September 26, 2001
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
Instructions: Please work in groups, and
acknowledge those you work with in your write up. Some of the problem below, such as
``factor a number'' can be quickly done with a computer. Feel free to
do so, unless otherwise stated.
- Let
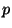 be a prime number and
be a prime number and 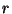 and integer such that
and integer such that
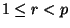 . Prove that
. Prove that 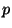 divides the binomial
coefficient
You may not assume that this coefficient is a integer.
divides the binomial
coefficient
You may not assume that this coefficient is a integer.
- Compute the following gcd's using a pencil and
the Euclidean algorithm:
- Using mathematical induction to prove that
then find a formula for
- What was the most recent prime year?
I.e., which of
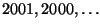 was it?
was it?
- Use the Euclidean algorithm to find integers
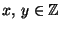 such that
[I did not tell you how to do this; see §1.8 of Davenport's book.]
such that
[I did not tell you how to do this; see §1.8 of Davenport's book.]
- Factor the year that you should graduate from Harvard
as a product of primes. E.g., frosh answer
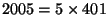 .
.
-
Write a PARI program to print ``Hello Kitty'' five times.
![\includegraphics[width=7em]{hkcomp.eps}](img13.png)
- Let
![$ f(x)\in\mathbb{Z}[x]$](img14.png) be a polynomial with integer coefficients.
Formulate a conjecture about when the set
be a polynomial with integer coefficients.
Formulate a conjecture about when the set
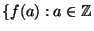 and $f(a)$ is prime
and $f(a)$ is prime 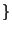 is infinite. Give computational evidence for your conjecture.
is infinite. Give computational evidence for your conjecture.
- Is it easy or hard for PARI to compute the gcd
of two random 2000-digit numbers?
- Prove that there are infinitely many primes of the form
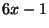 .
.
- Use PARI to compute
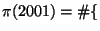
primes
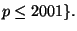
- The prime number theorem predicts that
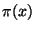 is
asymptotic to
is
asymptotic to 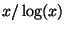 . How close is
. How close is 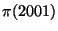 to
to
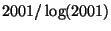 ?
?



Next: About this document ...
William A Stein
2001-10-11
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001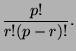
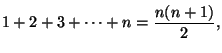
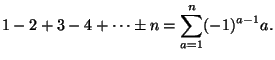
![\includegraphics[width=7em]{hkcomp.eps}](img13.png)