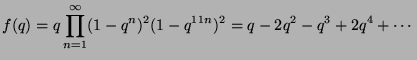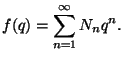Next: About this document ...
MATH 124: FINAL EXAMINATION
DUE AT 5PM ON SUNDAY, JANUARY 13TH, 2001
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
Instructions. Thoroughly justify all answers.
While taking the exam, please do not discuss these problems with
anyone else, and consult only those references that are explicitly
mentioned on the Math 124 web page. (If you inadvertently stumble
upon a solution while reading or studying for another class, e.g.,
Math 122, please make that clear in your solution.)
If you wish to use the result of a homework problem in the solution of
one of the problems below, include your solution of that homework
problem (a photocopy is acceptable). You may use any result that was
proved in the lecture notes or the course textbooks, but please give a
precise reference.
There are 10 problems, each worth 10 points, and problem 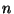 was
``inspired'' by homework assignment
was
``inspired'' by homework assignment 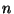 . Problems 3, 5(ii), 6, 7, and
10 would be difficult to do without a computer; for these problems,
you do not have to use PARI, though I recommend that you do.
. Problems 3, 5(ii), 6, 7, and
10 would be difficult to do without a computer; for these problems,
you do not have to use PARI, though I recommend that you do.
Turning in the exam. The exam is due on Sunday, January 13th at
5pm. Some of you don't have a key to the math department, so you
might not be able to go to my office (SC 515) and give me your exam.
If this is the case, call me at (617)495-1790 or (617)308-0144, and
I'll come downstairs and meet you at the elevator, and if that doesn't
work just slide it under my door on Monday morning (but no later!!).
- 1.
- The Fibonnaci numbers
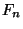 are defined as follows:
are defined as follows: 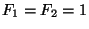 and
for
and
for 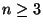 ,
,
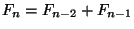 .
Prove that for every integer
.
Prove that for every integer 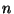 ,
the greatest common divisor of
,
the greatest common divisor of 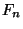 and
and 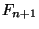 is
is 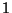 .
.
- 2.
- Let
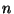 be an odd positive integer, and let
be an odd positive integer, and let
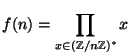 ,
where
,
where
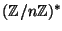 is the group of integers modulo
is the group of integers modulo 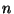 that are coprime to
that are coprime to 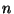 .
.
- (i)
- (5 points) Prove that
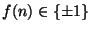 .
.
- (i)
- (5 points) Find a formula for
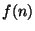 in terms of the number of
prime factors of
in terms of the number of
prime factors of 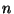 . [Hint: You might find the result of
Problem 4 on this exam useful.]
. [Hint: You might find the result of
Problem 4 on this exam useful.]
- 3.
- Consider the RSA cryptosystem
with public key
- (i)
- (3 points) A secret message has been encoded as the number
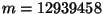 .
Encrypt the number
.
Encrypt the number 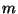 using the above RSA cryptosystem.
using the above RSA cryptosystem.
- (i)
- (4 points) Find the decoding key
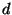 ; i.e., ``break'' this RSA cryptosystem.
; i.e., ``break'' this RSA cryptosystem.
- (i)
- (3 points) Decrypt
 . [Hint:
The answer won't look like total nonsense.]
. [Hint:
The answer won't look like total nonsense.]
- 4.
-
Let
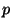 be an odd prime. Prove that
be an odd prime. Prove that
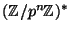 is cyclic for
all
is cyclic for
all 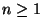 . (I.e., prove that there is an element of
. (I.e., prove that there is an element of
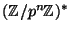 of order
of order
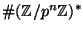 .)
.)
- 5.
- (i)
- (5 points) Evaluate the infinite continued fraction
![$ [3,\overline{1,4}]$](img22.png) .
.
- (i)
- (5 points) Determine the infinite continued fraction of
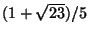 .
.
- 6.
- Write
 as a sum of two positive
integer squares.
as a sum of two positive
integer squares.
- 7.
- Determine the structure of the group
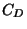 of equivalence
classes of primitive positive definite binary quadratic forms
of discriminant
of equivalence
classes of primitive positive definite binary quadratic forms
of discriminant 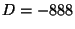 . Your answer should consist of
. Your answer should consist of 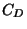 expressed
as a product of cyclic groups.
[Hint: Use the functions in forms.gp from Lecture 24.]
expressed
as a product of cyclic groups.
[Hint: Use the functions in forms.gp from Lecture 24.]
- 8.
- This problem describes a special case of a theorem that
was originally proven by Eichler and Shimura. The modularity theorem
says that a similar statement is true for every elliptic curve
over
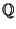 .
.
- (i)
- (3 points) Let
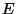 be the elliptic curve given by the equation
Let
be the elliptic curve given by the equation
Let
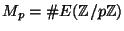 be the number of points on
be the number of points on 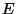 over
over
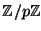 (don't forget the point at infinity). Calculate
(don't forget the point at infinity). Calculate
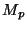 for
for
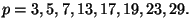
- (i)
- (3 points) Let
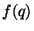 be the (formal) power series given by the infinite
product
Let
be the (formal) power series given by the infinite
product
Let 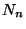 be the coefficient of
be the coefficient of 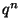 in
in 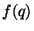 ,
Calculate
,
Calculate 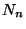 for
for 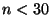 .
.
- (i)
- (4 points)
For each
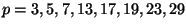 ,
compute the sum
,
compute the sum 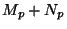 of the quantities
calculated in (i) and (ii), then formulate a conjecture as to what this
value should be for any prime
of the quantities
calculated in (i) and (ii), then formulate a conjecture as to what this
value should be for any prime 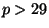 .
.
- 9.
- Let
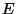 be the elliptic curve defined by the equation
be the elliptic curve defined by the equation
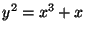 .
For each odd prime
.
For each odd prime 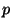 , let
, let 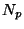 be
the number of points in the group
be
the number of points in the group
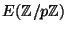 of points on
of points on 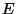 with coordinates in
with coordinates in
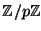 .
.
- (i)
- (5 points) For each odd prime
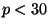 ,
find
,
find 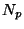 .
.
- (i)
- (5 points) Make a general conjecture for the value of
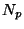 when
when
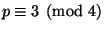 , and prove your conjecture.
, and prove your conjecture.
- 10.
- Demonstrate how to use the elliptic curve
factorization method to completely
factor the integer
 .
(You may use the isprime function of PARI to verify primality
of numbers.)
.
(You may use the isprime function of PARI to verify primality
of numbers.)
- 11.
- (Extra credit: automatic A in course, plus
fame and glory)
Let
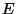 be the elliptic curve
be the elliptic curve
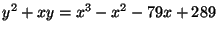 . Prove
that
. Prove
that
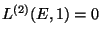 , where
, where
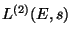 is the second derivative
of the
is the second derivative
of the 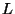 -series associated to
-series associated to 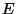 .
.



Next: About this document ...
William A Stein
2002-01-08
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001![]() was
``inspired'' by homework assignment
was
``inspired'' by homework assignment ![]() . Problems 3, 5(ii), 6, 7, and
10 would be difficult to do without a computer; for these problems,
you do not have to use PARI, though I recommend that you do.
. Problems 3, 5(ii), 6, 7, and
10 would be difficult to do without a computer; for these problems,
you do not have to use PARI, though I recommend that you do.
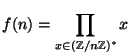 ,
where
,
where