


Next: The Torsion Subgroup
Up: Lecture 27: Torsion Points
Previous: Mordell's Theorem
As 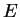 varies over all elliptic curves over
varies over all elliptic curves over
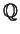 , what
are the possibilities for
, what
are the possibilities for
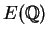 ? What finitely generated
abelian groups occur? Mordell's theorem implies that
where
? What finitely generated
abelian groups occur? Mordell's theorem implies that
where
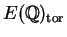 is the set of points of finite
order in
is the set of points of finite
order in
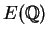 and
and
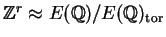 .
The number
.
The number 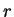 is called the rank of
is called the rank of 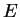 .
.
Subsections
William A Stein
2001-11-16